If you had watched the movie, Inception, you would have came across a never ending stairs made by Arthur (Joseph Gordon Levitt). In the dream, he creates an endless stairs that goes in circles. It is a Penrose stair, and such a stair can only depicted in two dimension, but cannot exist in three dimension. Strange right? Lets dive into the world of mind twisting paradoxes.
We will start by understanding what a paradox is. Paradox is a statement or proposition that seems to be logical, but becomes self contradictory on further investigation, or the other way around. They can be invalid in certain cases too. Each paradox will create numerous possibilities on critical thinking. There are paradoxes in mathematics, physics, philosophy etc. I handpicked a few that is quite strange and mind boggling.
1. Grandfather Paradox
If you time travelled to the past and killed your grandfather before he conceives any of your parent, it will makes you non existent, and therefore, you was not there to go back in time and kill your grandfather.
But you are existing, as you just came out from the time machine. That means your parents existed and your grandfather was not killed before conceiving your parent.
What just happened? Its a paradox. Modern scientific theories does not prevent any possibilities of time travelling. But still many physicists were convinced by this paradox to say, time travelling to past is impossible. That includes the most famous, Stephen Hawking. He even did an experiment in 2009. He threw a party in the University of Cambridge, with champagnes and balloons. Sadly no one turned up. Because he didn’t sent an invitation to any. Instead he sent the invitation after the party. He was actually expecting a time traveller to attend his party. He thought in future, someone somewhere will comes to know about this party that he conducted and attends it by time travelling. But no one came.
Many scientific theories popped out to solve the mystery of grandfather paradox like, Parallel Universe theory, Novikov self - consistency principle etc. It needs another elaborate post to explain those.
2. Ross-Littlewood Paradox
Ross-Littlewood paradox is a mathematical and logical paradox. It is famous by the names, 'ball vase problem', 'ping pong problem' etc. This problem was described by John E. Littlewood and Sheldon Ross and hence the name. Lets see the problem,
Suppose we have a vase of infinite height and we have infinite supply of balls. The time now is 30 seconds before noon. We are going to perform infinite number of steps before noon. The steps is as follows,
- Add 10 balls to vase from our supply
- Remove one ball
First step is done right now, that is 30 seconds before noon. Next step is done at the halfway time from now to noon. That is 15 seconds before noon. And the next step at the other halfway, that is 7.5 seconds till noon. And goes on. Thus we can do an infinite number of steps before noon, as we can divide the remaining time into half each time.
Now the question is, How many balls will be there in the vase at noon?
Need to think?
Take your time and come back if you gets a solution.
Here you are. The solution you got is absolutely correct. There will be infinite number of balls. But the surprising fact is that there is another solution at the same time that is mathematically correct. The answer is, vase will be empty. Mind blown? This inconsistency in the solution made this problem a paradox. Now let’s see how this weird answer came.
Suppose every Balls are numbered. From 1 to infinite number.
For the step 1, balls numbered 1 - 10 are placed in the vase and removed the Ball numbered 1.
In step 2, balls numbered 11 - 20 are placed in the vase and removed the Ball numbered 2.
In step 3, balls numbered 21 - 30 are placed in the vase and removed the Ball numbered 3.
.
.
.
And the steps continues to infinity. Now take any number. You can take any number, there will be a step of removing that numbered ball, because there are infinite number of steps. If the vase has n number of balls the step just before noon, there should be a steps to every ball including n within noon. You have to remember infinity + n is infinity and infinity - n is also infinity.
I know you have several questions in mind saying, its not true and is less intuitive. But mathematics works in mysterious ways. And that is why it became a paradox.
3. Monty Hall Problem
It is a probability paradox. The name was pinned from the presenter of an American television show (Let’s Make a Deal), Monty Hall. And the paradox is loosely based on this game show. The problem is,
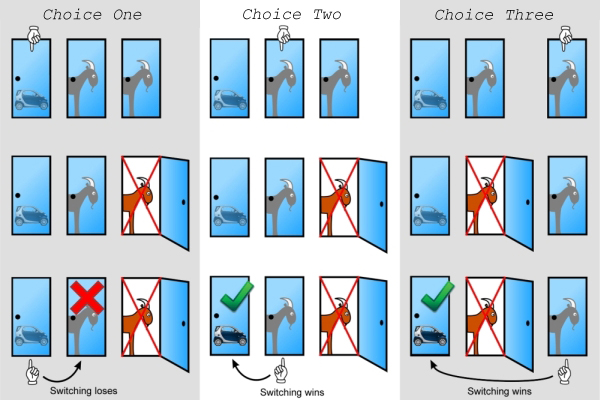
In a game show, you are given three doors to select any one of it. Behind the doors, there are a car, and two goats. If you finds the door with the car, you will win. First you have to select a door from the three. The host will then eliminate the remaining door that has goat. And he will give you a chance to switch the doors. So the question is, what gives you more chance of winning? Switching the doors or stay with your first decision?
Think about it and read the remaining after you gets a solution.
Answer is you will be successful if you switch the doors. Are you correct? The chances of winning by swapping is increased when the host eliminate another door that has a goat. In fact the host is helping us.
- If you selects a goat at the first time, then you are sure you will win by swapping the doors, after the host eliminates a door with goat.
- Initially, the probability of selecting the door with car is 1 out of 3. At the same time, the probability of selecting a goat is 2 out of 3.
- So you have most chance of selecting a goat initially. And when the host eliminates the other goat door, you are having a good chance of guessing the other door has the car as it has a probability of 2/3. While staying with the same door has probability of only 1/3.
Problem solved. It was initially thought of as a fifty-fifty chance of winning on swapping or not swapping, and the answer was seemed to be counterintuitive, even though its true. That is the reason this problem became a paradox.
4. Dichotomy Paradox
It is one of the Zeno’s paradoxes which is a set of philosophical problems. It is very similar to the ‘Achilles and Tortoise Paradox’. The problem is as follows,
If you want to catch a bus that is a finite distance away from you, you have to first reach half of the distance, then the other half, and then the other half, and so on to make infinite number of steps.
This problem deceive us to make a conclusion that you won’t catch the bus, but it is definitely false. So how it is proved mathematically? For that you have to know the Geometric series.
Geometric series, is a series that has a constant ratio between successive terms. An example is,
1/2 + 1/4 + 1/8 + 1/16 . . .
Each of the term is obtained by multiplying 1/2 with the previous one. Geometric series are infinite series with a finite sum. The solution for the above series is 1, which is finite.
Now let’s take the problem. When you are travelling half the distances continuously, you are actually performing a geometric series. Half the distance plus, the other half the distance and so on. That is the same as the geometric series written above. And the answer is a finite number for that series.
It is certain that you can travel a finite distance and hence proved the problem.
5. Omnipotence Paradox
It is yet another set of paradoxes that comes under philosophical paradoxes. It is based on the term omnipotent. Omnipotent is all powerful and with unlimited power. And this will lead to numerous paradoxes. There are different versions of this paradox. One of it is The Paradox of the Stone, and it states as,
“If God is omnipotent, can he make a stone so heavy that even he can’t lift?”
If he can, the he won’t become omnipotent as he cannot life it. If he cannot, then still he won’t be omnipotent as is not that powerful to make such a stone.
There are many discussions about this paradox. Some says the paradox itself contradicts. It is similar to ask, “What happens when an Unstoppable force meets an Unmovable object?”
That’s it for the paradoxes session. It’s more than enough to have a lot of thinking.
Learn a lot, think a lot.
No comments:
Post a Comment